观测矩阵、稀疏矩阵、稀疏基
压缩传感是对稀疏信号及进行观测得到少于数据量的观测值进行求解原数据量的内容。
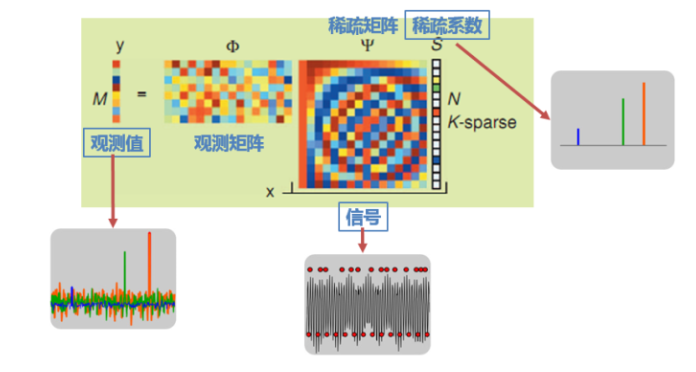
压缩感知需要满足两个条件:
- 信号的稀疏性,信号要能在某个稀疏域中表现出只有少量的非零信号,小于或等于k时,称为稀疏度为k。信号转化到该稀疏域中的方式称为稀疏矩阵或稀疏基、字典,通常是一组完备基,稀疏基的列向量成为原子。
- 不相关性。只有随机的亚采样才能实现信号的重建。奈奎斯特定理是采样平吕必须为最高2倍就要求了必须是等间距采样。不相关要求的是在观测矩阵与稀疏基的不相关,即测量矩阵的行向量不能用稀疏矩阵的列向量表示
测量矩阵与稀疏矩阵的乘积为传感矩阵。
通常情况下观测矩阵是已知,为什么不能直接求原始信号?稀疏矩阵知道具体数值吗?还是需要最稀疏值试出来选最优?
解释的更详细了点关于压缩感知的内容其中最后提到
如果要想采集很少一部分数据并且指望从这些少量数据中「解压缩」出大量信息,就需要保证:第一:这些少量的采集到的数据包含了原信号的全局信息,第二:存在一种算法能够从这些少量的数据中还原出原先的信息来。
第二部分已经被压缩感知的提出者解决,但是第一部分,很多随意压缩的模式是如何解决包含全部原信号的问题的?